Primer problema

$$\vec{A} = 5.00 \hat{i} + 3.00 \hat{j}$$ $$\vec{B} = 2.00 \hat{i} + 4.00 \hat{j} $$

Determine:

a. La magnitud del vector \(\vec{C}\) que tiene dos dimensiones, cuya componente en el eje \(y\) es igual a 6.00, si \(\vec{B}\bullet\vec{C} = 32\)

b. La magnitud de \(\vec{A}\times\vec{B} \)

Solución:

Nos piden la magnitud del vector C, debemos de aplicar los procedimientos para calcular el producto escalar o producto punto como si tuvieramos todos sus componentes pero agregando la incognita en i para el vector C y despejar.

$$\vec{B}\bullet\vec{C} = (2.00\hat{i} + 4.00\hat{j})\bullet(x\hat{i} + 6.00\hat{j}) $$ $$32 = (2.00\hat{i})(x\hat{i}) + (4.00\hat{j})(6.00\hat{j})$$ $$32 = 2x + 24$$ $$32 - 24 = 2x$$ $$\frac{8}{2} = x$$ $$4 = x$$ $$|\vec{C}| = \sqrt{(4.00\hat{i})^2 + (6.00\hat{j})^2}$$ $$|\vec{C}| = 7,21$$

Para el inciso b, debemos de realizar el producto cruz utilizando matrices para encontrar su resultado.

$$\vec{A}\times\vec{B} = \begin{pmatrix} i & j & k \\ 5 & 3 & 0 \\ 2 & 4 & 0 \\ \end{pmatrix} = +(i)\begin{pmatrix} 3 & 0 \\ 4 & 0 \\ \end{pmatrix} -(j)\begin{pmatrix} 5 & 0 \\ 2 & 0 \\ \end{pmatrix} + (k)\begin{pmatrix} 5 & 3 \\ 2 & 4 \\ \end{pmatrix}$$ $$\vec{A}\times\vec{B} = (\hat{i})[(3)(0)-(4)(0)] -(\hat{j})[(5)(0)-(2)(0)]+(\hat{k})[(5)(4)-(2)(3)]$$ $$\vec{A}\times\vec{B} = 0\hat{i} - 0\hat{j} + 14\hat{k}$$ $$|\vec{A}\times\vec{B}| = \sqrt{(0)^2 + (0)^2 + (14)^2} = 14$$

Segundo problema

Para la gráfica posición-tiempo que se muestra, determine:

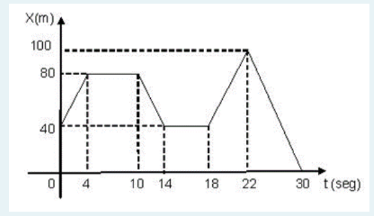
a. La distancia en m, recorrida en t = 10.0s y t = 30.0s

b.La magnitud de la velocidad media, en m/s, entre t = 0 y t = 18.0s

c.La rapidez, en m/s, en t = 25.0s

Solución:

Para poder encontrar la distancia en un intervalo de tiempo en un gráfico posición - tiempo debemos de estudiar las posiciones de la partícula entre las posiciones finales e iniciales, realizando lo siguiente:

$$D = (x_{tiempo}, y_{posición})$$ $$D_{y} = y_{f} - y_{i}$$ $$D_{14-10} = 40 - 80 = -40$$ $$D_{18-14} = 40 - 40 = 0$$ $$D_{22-18} = 100 - 40 = 60$$ $$D_{30-22} = 0 - 100 = -100$$ $$D_{total} = |-40| + 0 + 60 + |-100| = 200m$$

Para poder encontrar la magnitud de la velocidad media debemos de encontrar la posición entre el intervalo de tiempo asignado teniendo mucho cuidado la posición final y la inicial ya que puede crear confusión. Siendo así el procedimiento:

$$V = \frac{\Delta{r}}{\Delta{t}}$$ $$D_{4-0s} = 80 - 40 = 40m$$ $$D_{10-4s} = 80 - 80 = 0m$$ $$D_{14-10s} = 40 - 80 = -40m$$ $$D_{18-14s} = 40 - 40 = 0m$$ $$D_{total} = 40 + 0 -40 + 0 = 0m$$ $$v = \frac{0m}{18 - 0s} = 0 \frac{m}{s}$$

Recuerda que para poder calcular la magnitud de la velocidad media de una particula en un intervalo de tiempo, es necesario usar el desplazamiento, la sumatoria de sus posiciones incluyendo los signos negativos.

Ahora para el último inciso usaremos la ecuación de pendiente de una recta ya que podemos aplicarlo en este tipo de ejercicio ya que su forma geometrica es un triángulo:

$$m = \frac{y_{f} - y_{i}}{x_{f} - x_{i}}$$ $$m = \frac{100 - 0}{30 - 22} = \frac{100}{8} = 12.5\frac{m}{s}$$

Es muy posible que en un examen universitario el procedimiento anterior sea tomado como: "El procedimiento no es considerado correcto y por lo tanto será anulada su respuesta". Para evitarlo usaremos otro método que llevará a la respuesta correcta usando triángulos semejantes:

$$\frac{H_{altura}}{\Delta{t}} = \frac{h_{altura}}{\Delta{t}}$$ $$\frac{100}{30-22} = \frac{h}{30-25}$$ $$\frac{100}{8} = \frac{h}{5}$$ $$(100)(5) = h(8)$$ $$h = 62.5m$$ $$m = \frac{\Delta{h}}{\Delta{t}} = \frac{h_{final} - h_{inicial}}{t_{final} - t_{inicial}} = \frac{62.5 - 0}{30-25}= \frac{62.5}{5} = 12.5\frac{m}{s}$$

Tercer problema

la posición de un dron está descrita por:

$$\vec{r} = [5.00 \frac{m}{s}t]\hat{i} + [7.00 \frac{m}{s}]\hat{j} + [4.00 \frac{m}{s^{2}} t^2]\hat{k}$$

Determine:

a. la magnitud de la velocidad media, en \(m/s\), entre t = 0 y t = 7.00s

b. La rapidez, en \(m/s\), en t = 5.00s

c. La magnitud de la aceleración, en \(m/s\), en t = 3.00s

Solución:

Aplicamos la ecuación de velocidad media \(\bar{v} = \frac{\Delta r}{\Delta t}\) teniendo cuidado ya que la posición del dron está dada como un vector, ya que la velocidad media necesita el cambio en el desplazamiento no es necesario utilizar la primera derivada para encontrar la velocidad media.

$$\vec{r}(0) = 5.00 \frac{m}{s} (0) \hat{i} + 7.00 \frac{m}{s} \hat{j} + 4.00 \frac{m}{s} (0) \hat{k}$$ $$\vec{r}(5) = 5.00 \frac{m}{s} (7) \hat{i} + 7.00 \frac{m}{s} \hat{j} + 4.00 \frac{m}{s} (7)^2 \hat{k}$$

Se obtienen los vectores:

$$\vec{r}(0) = 7.00 \frac{m}{s}\hat{j}$$ $$\vec{r}(5) = 35.0 m \hat{i} + 7.00 \frac{m}{s} \hat{j} + 196.0 m \hat{k}$$

Encontrando el desplazamiento:

$$\Delta r = \vec{r}(5) - \vec{r}(0)$$ $$\Delta r = 35.0 m \hat{i} + 7.00 \frac{m}{s} \hat{j} + 196.0 m \hat{k} - 7.00 \frac{m}{s}\hat{j}$$ $$\Delta r = 35.0 m \hat{i} + 196.0 m \hat{k}$$

Obtenemos la magnitud del vector para poder dividirlo entre el intervalo de tiempo encontrando la velocidad media del dron.

$$\bar{v} = \frac{\sqrt{35^2 + 196^2}}{7-0} = \frac{199.100}{7} = 28.4 \frac{m}{s}$$

Ahora encontraremos la rapidez cuando son cinco segundos, para esto necesitaremos derivar una vez el vector desplazamiento.

$$\vec{r} = \frac{\Delta v}{\Delta t} = 5.00 \frac{m}{s} \hat{i} + 8.00 \frac{m}{s} t \hat{k}$$ $$\vec{r} = \frac{\Delta v}{\Delta t} = 5.00 \frac{m}{s} \hat{i} + 8.00 \frac{m}{s} (5.00) \hat{k}$$ $$\vec{r} = \frac{\Delta v}{\Delta t} = 5.00 \frac{m}{s} \hat{i} + 40.00 \frac{m}{s} \hat{k}$$ $$v = \sqrt{5^2 + 40^2} = \sqrt{1625} = 40.31 m/s$$

En el último inciso, para poder encontrar la acerleración derivaremos una vez más partiendo del vector velocidad.

$$[\vec{r}]'' = a = 8.00 \frac{m}{s}$$ $$[\vec{r}(3.00)]'' = a = 8.00 \frac{m}{s}$$

Cuarto problema

Un helicóptero sube a una velocidad constante de 70.00 m/s, cuando se encuentra a una altura de 40.0 m, deja caer una caja. Determine:

a. La rapidez de la caja, en m/s en el momento de llegar al suelo.

b. La alura máxima de la caja, en m, desde el suelo.